MATRICES

MATRICES

Se puede definir a una matriz como un conjunto de elementos (numeros) ordenados en filas y columnas

En matemáticas, una matriz es un arreglo bidimensional de números, y en su mayor generalidad de elementos de un anillo. Las matrices se usan generalmente para describir sistemas de ecuaciones lineales, sistemas de ecuaciones diferenciales o representar una aplicación lineal (dada una base). Las matrices se describen en el campo de la teoría de matrices.

Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar las aplicaciones lineales; en este último caso las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.

Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.

Ejemplo:

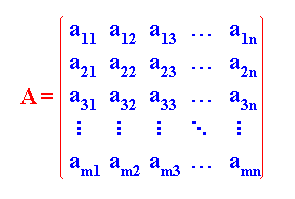
Esta es una matriz de (m) filas y (n) columnas, es decir de dimension ( m x n). Esta matriz también se la puede representar de la forma siguiente A = (aij) m x n.

Si el numero de filas y de columnas es igual a (m = n), entonces se dice que la raiz es de orden (n).

2. IGUALDAD DE MATRICES
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales
	Para que las matrices  A  y  B  sean iguales, se tiene que cumplir que  a = 7  y  b = 5.

TIPOS DE MATRICES

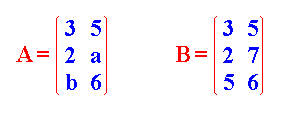
• Matriz Fila
• Matriz Columna
• Matriz Rectangular
• Matriz Transpuesta
• Matriz Nula
• Matriz Cuadrada

CLASES DE MATRICES CUADRADAS

1.     Matriz triangular superior

2.     Matriz triangular inferior

3.     Matriz diagonal

4.     Matriz escalar

5.     Matriz identidad o unidad

6.     Matriz regular

7.     Matriz singular

8.     Matriz idempotente

9.     Matriz involutiva

10.  Matriz simétrica

11.  Matriz antisimetrica o hemisimetrica

12.  Matriz ortogonal