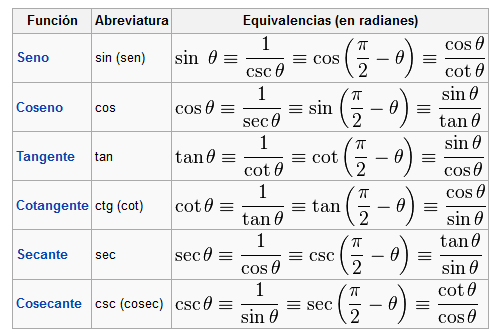
CONCEPTO:
En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.
Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo
asociado a sus ángulos. Las funciones trigonométricas son funciones
cuyos valores son extensiones del concepto de razón trigonométrica en un
triángulo rectángulo trazado en una circunferencia unitaria
(de radio unidad). Definiciones más modernas las describen como series
infinitas o como la solución de ciertas ecuaciones diferenciales,
permitiendo su extensión a valores positivos y negativos, e incluso a
números complejos.
6 Funciones trigonométricas

TRIANGULO RECTÁNGULO
 , del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:- La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
- El cateto opuesto (a) es el lado opuesto al ángulo
 .
. - El cateto adyacente (b) es el lado adyacente al ángulo
 .
.
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:
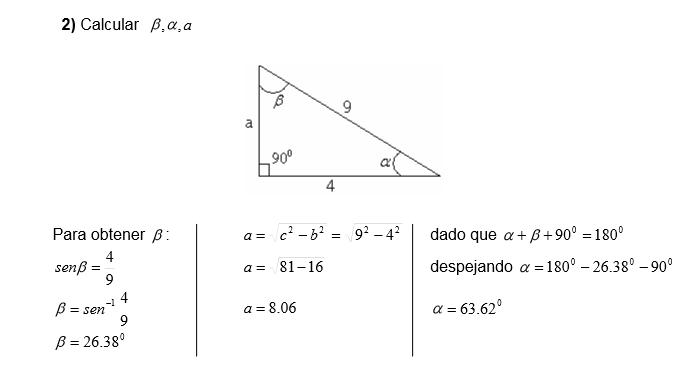
ejercicios:
........................................................................










 es siempre constante. Se calcula mediante la ecuación:
es siempre constante. Se calcula mediante la ecuación: 

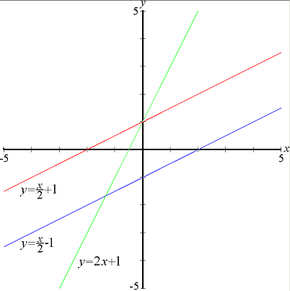
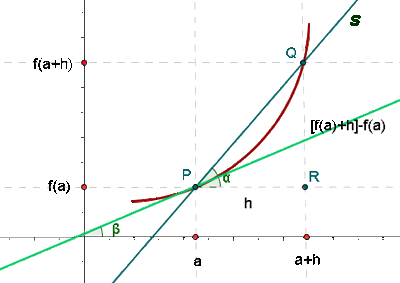
 es la tangente del ángulo que forma la recta con el eje de abscisas X.
es la tangente del ángulo que forma la recta con el eje de abscisas X. y tiene la pendiente dada
y tiene la pendiente dada 
 y que tiene una pendiente de
y que tiene una pendiente de  .
.






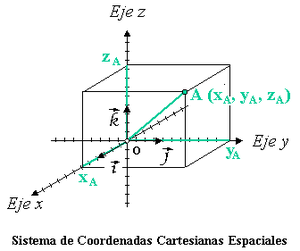
 se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho punto (
se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho punto ( ) sobre un eje determinado:
) sobre un eje determinado:
 ) tal que:
) tal que: , cuyo módulo es
, cuyo módulo es  .
.


