MATEMÁTICAS M3: SISTEMA DE COORDENADAS CARTESIANAS

COORDENADAS CARTESIANAS

CONCEPTO:

En geometría, un sistema de coordenadas es un sistema que utiliza uno o más números (coordenadas) para determinar unívoca mente la posición de un punto o de otro objeto geométrico.¹
El orden en que se escriben las coordenadas es significativo y a veces se las identifica por su posición en una tupla ordenada; también se las puede representar con letras, como por ejemplo «la coordenada-x». El estudio de los sistemas de coordenadas es objeto de la geometría analítica, permite formular los problemas geométricos de forma "numérica".²
Un ejemplo corriente es el sistema que asigna longitud y latitud para localizar coordenadas geográficas. En física, un sistema de coordenadas para describir puntos en el espacio recibe el nombre de sistema de referencia.

Sistema de coordenadas cartesianas

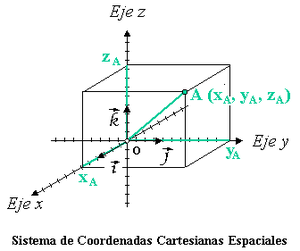
En un espacio euclídeo un sistema de coordenadas cartesianas se define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es un sistema bidimensional o tridimensional (análogamente en $\scriptstyle \mathbb{R} ^{n}$ se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho punto ( ${\mathbf r}_{{\text{A}}}={\text{OA}}\,$ ) sobre un eje determinado:

${\mathbf r}_{{\text{A}}}={\text{OA}}=(x_{{\text{A}}},y_{{\text{A}}},z_{{\text{A}}})$

Cada uno de los ejes está definido por un vector director y por el origen de coordenadas. Por ejemplo, el eje x está definido por el origen de coordenadas (O) y un vector ( ${\mathbf {i}}\,$ ) tal que: