TAUTOLOGICAS _ CONTRADICCIONES y CONTINGENCIAS

DEFINICIÓN

Una formula (f)se dice tautologia si para cualquier interpretación conjunto de letras proporcionales, su significado valor de verdad es (v) se dice contradicción, si para cualquier interpretación su significado es (f) y se dice contingencia si no es tautologia y contradicción. 

solución: 

Entonces (f) es tautologia

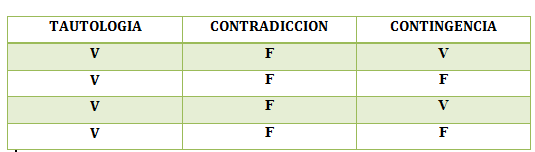
SE LAS RECONOCE DE LA SIGUIENTE FORMA: 

Entonces f es contingencia

EQUIVALENCIAS DE NEGACIÓN

P: Fatima tiene 20 años 

Q: Fatima vive en naranjito

p^q

                      

Fatima tiene 20 años o vive en Naranjito  (v)

Fatima no tiene 20 años y no vive en naranjito (f)

2._ Joselyn es bonita (v)

      Jonny tiene moto (v)

p ^ q → Joselyn es bonita y Johnny tiene moto  (v)

¬ (p ^ q) = ¬ p v ¬ q

3._ P: La UNEMI tiene categoría B 

      Q: La UNEMI tiene estudiantes sobresalientes

p  →  q 

Si la UNEMI tiene categoría B entonces tiene estudiantes sobresalientes. 

¬(p→q) = p^¬q 

La UNEMI tiene categoría B y no tiene estudiantes sobresalientes.

CONTRARECIPROCO

Si la UNEMI no tiene estudiantes sobresalientes entonces no tiene          categoría B.

P: Vanesa es risueña (v)

Q: Rebeca ama a Diego (v) 

 P → Q

Si Vanesa es risueña entonces Rebeca ama a Diego

Si Rebeca no ama a Diego entonces Vanesa no es risueña

                                          DOBLE IMPLICACIÓN

Vanesa no es risueña o Rebeca ama a Diego

P: Hoy es miércoles 

Q: Hoy tengo clase de matemáticas

Hoy es miércoles si y solo si tengo clase de matemáticas.

Si hoy es miércoles entonces tengo clases de matemáticas y si tengo clases de matemáticas entonces hoy es miércoles.

┐q →┐p = q ^ ┐p     (v y f)

EQUIVALENCIAS