CONJUNTOS

LOS CONJUNTOS 

Es una agrupación de objetos que poseen alguna característica común. pero no solo nos referimos a cosas físicas como: lapices, libros, calculadoras, etc. sino también conjunto de números, letras, entre otros.

ejemplo: ( a, e, i, o, u,) 

A los objetos se les llama elementos del conjunto .

Si tenemos el siguiente conjunto:

c = ( 1, 2, 3, 4 ) decimos q los elementos del conjunto "c" son 

los números 1, 2, 3, 4 .

Con frecuencia, utilizamos letras mayúsculas A, B, C, para designar el conjunto y letras minúsculas a, b, c, d.... para referirnos a los elementos que forman parte de ese conjunto. 

Todos los conjuntos se escriben entre llaves así: 

Determinación de un Conjunto

Los conjuntos pueden definirse por extensión o por comprensión.

Extensión  

Se escribe los elementos que forman parte del conjunto, uno por uno separados por una coma y entre paréntesis de llaves.

c ={norte, sur, este, oeste}

Comprensión

Decimos que un conjunto es determinado por comprensión, cuando se da una propiedad que se cumpla en todos todos los elementos del conjunto y solo de ellos.

Se lee por tal que x:

C ={ x/x  es u punto cardinal }

D ={ x/x es un día de la semana }  

M ={ x/x es un mes del año } 

C ={ x/x es un color }

E ={ x/x es una estación del año } 

B ={ x/x es un número impar menor que 10 }

C ={ x/x es una letra de la palabra feliz }

Para definir un conjunto por comprensión, es necesario saber algunos símbolos matemáticos.

1.- < "menor que"

2.- > "mayor que"

3.-  / "y"

Decimos que dos conjuntos son iguales, solo si contienen los mismos objetos.

A={ a, e, i, o, u } 

B={ a, e, i, o, u, a }

c={ x/x es una vocal } 

Como se pueden ver los tres conjuntos (A,B y C) son iguales, por lo que podemos darnos cuenta que podemos describir un mismo conjunto de diferentes maneras.

Ejemplos de extensión                                           Ejemplos por comprensión

A ={ a ,e, i, o, u }                                    A ={ x/x es una vocal }

B ={ 1, 3, 5, 7, 9 }                                    B={ x/x es un número impar menor que 10 }

D ={ f, e, l, i, 2 }                                      D ={ x/x es una letra de la palabra feliz }

E ={ b, c, d ,f, g, h, j, k }                         E ={ x/x es una consonante }

G ={ venus, marte}                                   G ={ x/x es un planeta }

Aplicaciones de la Teoría de Conjunto

Números de elementos de un conjunto

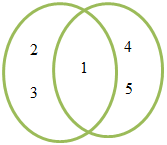
A ={ 1, 2, 3}

B ={ 1, 4, 5}

A∩B ={ 1 }

Fórmula

∩(AB) = ∩(A) + (B) - ∩(A ∩ B)