LA RECTA
En geometría euclidiana, la recta o la línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea
más corto que une dos puntos). También se describe como la sucesión
continua e indefinida de puntos en una sola dimensión, es decir, no
posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano.
Son considerados conceptos hipocorísticos ya que su definición sólo es
posible a partir de la descripción de las características de otros
elementos similares. Así, es posible elaborar definiciones basándose en
los postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
En geometría analítica las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano cartesiano. En dicha expresión m
es denominada la "pendiente de la recta" y está relacionada con la
inclinación que toma la recta respecto a un par de ejes que definen el
plano. Mientras que b es el denominado "término independiente" u
"ordenada al origen" y es el valor del punto en el cual la recta corta
al eje vertical en el plano.
Características de la recta
- La recta se prolonga indefinidamente en ambos sentidos.
- En geometría euclidiana, la distancia más corta entre dos puntos es la línea recta.
- La recta puede definirse como el conjunto de puntos situados a lo largo de la intersección de dos planos.
Ecuación de la recta
En un plano cartesiano,
podemos representar una recta mediante una ecuación, y determinar los
valores que cumplan determinadas condiciones, por ejemplo, las de un
problema de geometría.
Pendiente y ordenada al origen
En una recta, la pendiente  es siempre constante. Se calcula mediante la ecuación:
es siempre constante. Se calcula mediante la ecuación:
 |
Esta forma de obtener la ecuación de una recta se suele utilizar cuando se conocen su pendiente y las coordenadas de uno de sus puntos, o cuando se conocen sólo los dos puntos, por lo que también se le llama ecuación de la recta conocidos dos puntos, y se le debe a Jean Baptiste Biot. La pendiente
 es la tangente del ángulo que forma la recta con el eje de abscisas X.
es la tangente del ángulo que forma la recta con el eje de abscisas X.La ecuación de la recta que pasa por el punto
 y tiene la pendiente dada
y tiene la pendiente dada  es:
es:- Ejemplo
- La ecuación de la recta que pasa por el punto A
 y que tiene una pendiente de
y que tiene una pendiente de  .
.

   
|
PENDIENTE DE UNA RECTA
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Se denota con la letra m.
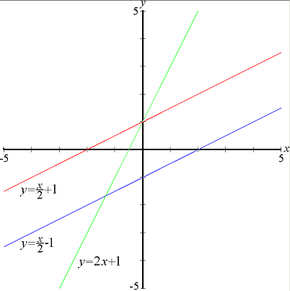
Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.
Cálculo de la pendiente

Pendiente dado el ángulo
Pendiente dado el vector director de la recta
Pendiente dados dos puntos
Pendiente dada la ecuación de la recta.
Ejemplos
La pendiente de la recta que pasa por los puntos A(2, 1), B(4, 7) es:
La recta que pasa por los puntos A(1, 2), B(1, 7) no tiene pendiente, ya que la división por 0 no está definida.
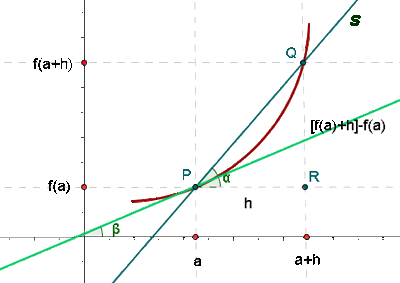
La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto.




No hay comentarios:
Publicar un comentario