MATEMÁTICAS M3: VALOR ABSOLUTO

VALOR ABSOLUTO

En matemática, el valor absoluto o módulo de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo o negativo. Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.

Misma distancia al origen.

Valor absoluto de un número real a, se escribe |a|, es el mismo número a cuando es positivo o cero, y opuesto de a, si a es negativo.

Valor absoluto de un número real

Formalmente, el valor absoluto o módulo de todo número real $a\,$ está definido por:

$|a| = \left \{ \begin{array}{rcl} a, & \mbox{si} & a \ge 0 \\ -a, & \mbox{si} & a < 0 \end{array} \right .$

Por definición, el valor absoluto de $a\,$ siempre será mayor o igual que cero y nunca negativo.

Desde un punto de vista geométrico, el valor absoluto de un número real $a\,$ es siempre positivo o cero, pero nunca negativo.

En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos.

De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.

Propiedades fundamentales del valor absoluto

$\|a\| \ge 0$	No negatividad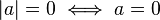
$\|a\| = 0 \iff a = 0$	Definición positiva
$\|ab\| = \|a\| \|b\|\,$	Propiedad multiplicativa
$\|a+b\| \le \|a\| + \|b\|$	Desigualdad triangular (Véase también Propiedad aditiva)

Otras propiedades

$\|-a\| = \|a\|\,$	Simetría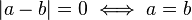
$\|a-b\| = 0 \iff a = b$	Identidad de indiscernibles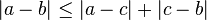
$\|a-b\| \le \|a-c\| + \|c-b\|$	Desigualdad triangular
$\|a-b\| \ge \|\|a\| - \|b\|\|$	(equivalente a la propiedad aditiva)
$\left\| \frac {a}{b}\right\| = \frac {\|a\|}{\|b\|} (si \ b \ne 0)$	Preservación de la división (equivalente a la propiedad multiplicativa)